1.
Число 2013 перемножено само на себя 2013
раз и к полученному результату прибавлено число 2013, записанное в обратном
порядке. Простое или составное получилось число, и если составное, то каков его
наименьший простой делитель?
Решение.
Числа 2013 и 3102 делятся на 3 (это можно проверить непосредственно или
заметить, что сумма их цифр делится на 3) Поэтому получившееся число делится на
3. На 2 оно не делится, так как является суммой нечётного (2013 х 2013 х ... х
2013) и чётного (3102) чисел.
Ответ:
Составное. Наименьший простой делитель равен 3.
1.
Можно ли завернуть в платок размером 3x3
куб со стороной единица, не разрезая платок?
Решение. На рисунке
изображён платок. В центральный квадрат нужно положить кубик, тогда квадраты А,
В, С, D закроют боковые грани кубика, а пятиугольников Е хватит,
чтобы они все вместе закрыли верхнюю грань кубика, так как высота каждого
пятиугольника больше половины стороны квадрата. Необозначенные участки платка
разрезать не придётся.
Ответ: Да, можно.
3.
В городе Мухоморске телефонные номера
состоят из шести цифр, причём первая цифра номера не может быть восьмёркой или
нулём. Однако каждая «крутая» фирма в этом городе считает ниже своего
достоинства иметь в телефоне меньше пяти идущих подряд одинаковых цифр. Сколько
«крутых» фирм можно зарегистрировать в Мухоморске?
Решение. Заметим, что фактически «крутые» мухоморские номера
состоят из двух цифр, только одна из них повторена еще 4 раза. Например,
«крутой» номер 35-55-55 фактически есть 35, а номер 77-77-71 фактически есть
71. Отметим, что каждому фактическому двузначному номеру с различными цифрами
(первая цифра не 0 и не 8) соответствуют два «крутых», например, номеру 31 -
«крутые» номера 33-33-31 и 31-11-11. Фактическому двузначному номеру с
одинаковыми цифрами соответствует один «крутой» номер. Посмотрим, какие
фактические двузначные номера могут быть у «крутых» фирм. Это номера с 10 до 79
(70 номеров), из них 7 имеют одинаковые цифры. Ещё есть номера с 90 по 99.
Первой группе соответствуют (70-7)х2+7=133 «крутых» номера, а второй группе -
19. Если каждая «крутая» фирма имеет только один «крутой» номер, то таких фирм
может быть 152. Если не один - то меньше.
Ответ:
152 фирмы.
4.
Какое наибольшее число точек пересечения
может быть у двух четырёхугольников (четырёхугольником мы называем замкнутую
четырёхзвенную ломаную линию без самопересечений)?
Решение. В четырёхугольнике 4 стороны, и каждая из них может
пересечь не более 4 сторон другого четырёхугольника. То есть больше, чем 16
точек пересечения, быть не может. Вариант 16 точек пересечения двух
невыпуклых
четырёхугольников приведён на рисунке.
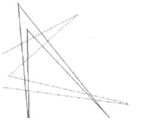
Ответ: 16.
5.
Сколькими способами можно расставить на
шахматной доске чёрного и белого королей так, чтобы они не били друг друга (не
стояли на соседних клетках)? Примечание: расстановки, при которых чёрный и
белый короли меняются местами, считаются разными.
Решение. Подсчитаем сначала, сколько всего расположений двух
разноцветных королей на шахматной доске. Чёрного короля можно поставить на 64
свободных клетки, и каждый раз белого короля - на 63 оставшиеся клетки. Всего
64 х 63 = 4032 расположения. Посмотрим теперь, в скольких случаях они бьют друг
друга. Если чёрный король стоит на угловых полях а 1, а8, h1, h8, то белый король может
стоять на трёх окаймляющих угловое поле полях. Всего 4x3 = 12 вариантов. Если
чёрный король стоит на краю доски, но не в углу (таких полей 6 X 4 = 24), то
белый король должен стоять на одном из пяти полей, примыкающих к крайнему полю.
Всего таких вариантов 4x6 х5 = 120. И наконец, если чёрный король не
соприкасается с краем доски (таких полей 6x6 = 36), то для белого
- 8 возможностей. Всего таких расстановок 36 х 8 = 288. Вариантов, когда два
короля не бьют друг друга, будет 4032 - 12 - 120 - 288 = 3612.
Ответ: 3612.