Темы для Юкоз

Введение.

Пифагор (VI в. до н. э.) — не только самый популярный ученый, но и самая загадочная личность, человек-символ и человек-фантом, фи­лософ и пророк. Основоположник дедуктивного научного знания — мате­матики и родоначальник многих мистических учений, учредитель рели­гиозно-этического братства и создатель научно-философской школы, ставшей воистину союзом Истины, Добра и Красоты.

Пифагор — едва ли не самый популярный ученый за всю историю человечества. Если сотни миллионов учащихся умножить на сотни исписываемых ими тетрадей в клеточку, с каждой из которых смотрит на нас таблица Пифагора, то получится астро­номическая цифра. Ни одно имя ученого не повторяется так часто. Но суть, конечно, не в этих арифметических упражне­ниях в духе «статистика мироздания».

Пифагор был не только ученым, основателем первой научной школы. Он был и властителем дум, проповедником собствен­ной «пифагорейской» этики, философом, которого по силе духа и силе воздействия можно сравнить разве что с его великими современниками: Конфуцием, Буддой и, возможно, Заратуштрой. Но в отличие от последних Пифагор создал самую яркую и самую современную «религию»: Пифагор воспитал в челове­честве веру в могущество разума, убежденность в познаваемости природы, уверенность в том, что ключом к тайнам мироздания является математика.

Историю человечества всегда связывали с именами царей и полководцев. Между тем выдающиеся ученые могут напра­вить цивилизацию по совершенно новому руслу. Сегодня, к несчастью, страшной ценой — ценой угрозы ядерной смерти человечества эта мысль стала очевидной для всех. Но кто и сегодня позволит себе назвать Ньютона самой значительной фигурой XVII в.? А ведь именно Ньютон определил развитие всей культуры последних трех столетий. И как Ньютон 300 лет назад раскрыл перед человечеством окно во Вселенную, так и Пифагор 2500 лет назад направил людей по пути торжества Разума.

БИОГРАФИЯ.

Древнегреческий мыслитель, религиозный и политический деятель.

Скудные сведения о его жизни и учении трудно отделить от легенд, представляющих философа как полубога, совершенного мудреца, наследника всей античной и ближневосточной науки, чудотворца и мага.

Пифагор покинул родной остров Самос в знак протеста против тирании Поликрата. Возможно, путешествуя, он действительно побывал в Египте и Вавилоне (исследователи предполагают, что он был посвящен в различные тайные доктрины). В зрелом возрасте, примерно на сороковом году жизни, философ поселился в южноиталийском городе Кротон, где основал строго закрытое общество своих последователей, уже при жизни почитавших его как высшее существо. Это было этико-религиозное братство, получившее широкое распространение и имевшее целью нравственное обновление и очищение религиозных воззрений. Впоследствии оно подвергалось жестоким преследованиям.

Доктрины и открытия Пифагора, сохранившиеся в устной традиции, невозможно отделить от идей его последователей, любивших приписывать философу собственную умственную инициативу.

В области математики Пифагору приписывается систематическое введение доказательств в геометрию, создание учения о подобии, доказательство теоремы, носящей его имя, построение некоторых правильных многоугольников и многогранников. С его именем связывают также учение о четных и нечетных, простых и составных, фигурных и совершенных числах, об арифметических, геометрических и гармонических пропорциях.

Пифагорейцы принимали шарообразность земли и ее движение вокруг центрального огня — источника света и тепла; вокруг него же движутся и другие светила, которые производят при этом музыкально-благозвучный шум, так называемую «гармонию сфер».

Пифагорейцы признавали бессмертие души и ее постепенное очищение (катарсис) посредством постижения музыкально-числовой структуры космоса.

ТЕОРЕМА ПИФАГОРА

                    Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с теоремой Пифагора. Пожалуй, даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о «пифагоровых штанах» — квадрате на гипотену­зе, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора триедина: это простота — красота — значимость. В самом деле, теорема Пифагора проста, но не очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.), свиде­тельствует о гигантском числе ее конкретных реализаций.

                       Открытие теоремы Пифагором окружено ореолом красивых легенд. Прокл, комментируя последнее предложение I книги «Начал» Евклида, пишет: «Если послушать тех, кто любит повторять древние легенды, то придется сказать, что эта теорема восходит к Пифагору; рассказывают, что он в честь этого открытия принес в жертву быка». Впрочем, более щедрые сказители одного быка превратили в одну гекатомбу, а это уже целая сотня. И хотя еще Цицерон заметил, что всякое пролитие крови было чуждо уставу пифагорейского ордена, легенда эта прочно срослась с теоремой Пифагора и через две тысячи лет продолжала вызывать горячие отклики.

                        Так, оптимист Михайло Ломоносов (1711 —1765) писал: «Пифагор за изобретение одного геометрического правила Зевесу принес на жертву сто волов. Но ежели бы за найденные в нынешние времена от остроумных математиков правила по суеверной его ревности поступать, то едва бы в целом свете столько рогатого скота сыскалось».

                              А вот ироничный Генрих Гейне (1797—1856) видел развитие той же ситуации несколько иначе: «Кто знает! Кто знает! Возможно, душа Пифагора переселилась в беднягу кандидата, который не смог доказать теорему Пифагора и провалился из-за этого на экзаменах, тогда как в его экзаменаторах обитают души тех быков, которых Пифагор, обрадованный открытием своей теоремы, принес в жертву бессмертным богам».

                  И хотя сегодня теорема Пифагора обнаружена в различных частных задачах и чертежах: и в египетском треугольнике в папирусе времен фараона Аменемхета I (ок. 2000 до н.э.), и в вавилонских клинописных табличках эпохи царя Хаммурапи (XVIII в. до н. э.), и в древнейшем китайском трактате «Чжоу-би суань цзинь» («Математический трактат о гномоне»), время создания которого точно не известно, но где утверждается, что в XII в. до н. э. китайцы знали свойства египетского треугольника, а к VI в. до н. э,—и общий вид теоремы, и в древнеиндийском геометрическо-теологическом трактате VII — V вв. до н.э. «Сульва сутра» («Правила веревки»),— несмотря на все это, имя Пифаго­ра столь прочно сплавилось с теоремой Пифагора, что сейчас просто невозможно представить, что это словосочетание распа­дется. То же относится и к легенде о заклании быков Пифагором. Да и вряд ли нужно препарировать историко-математическим скальпелем красивые древние предания.

                    Сегодня принято считать, что Пифагор дал первое доказатель­ство носящей его имя теоремы. Увы, от этого доказательства также не сохранилось никаких следов. Поэтому нам ничего не остается, как рассмотреть некоторые классические доказательства теоремы Пифагора, известные из древних трактатов. Сделать это полезно еще и потому, что в современных школьных учебниках дается алгебраическое доказательство теоремы. При этом бесслед­но исчезает первозданная геометрическая аура теоремы, теряется та нить Ариадны, которая вела древних мудрецов к истине, а путь этот почти всегда оказывался кратчайшим и всегда красивым.           Итак,

Теорема Пифагора. Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах.

Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треуголь­ников (рис. 1), чтобы убедиться в справедливости теоремы. Например, для Д/4ВС: квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах,— по два. Теорема доказана.

Древнекитайское доказательство. Математические трактаты Древнего Китая дошли до нас в редакции II в. до н. э. Дело в том,

что в 213 г. до н.э. китайский император Ши Хуан-ди, стремясь ликвидировать прежние традиции, приказал сжечь все древние книги. Во II в. до н.э. в Китае была изобретена бумага и одновре­менно начинается воссоздание древних книг. Так возникла «Ма­тематика в девяти книгах» — главное из сохранившихся мате- матико-астрономических сочине­ний.

В IX книге «Математики» по­мещен чертеж (рис. 2), до­казывающий теорему Пифагора. Ключ к этому доказательству

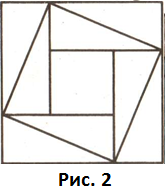
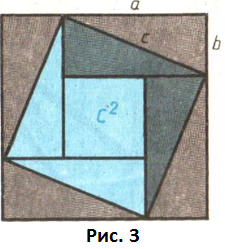
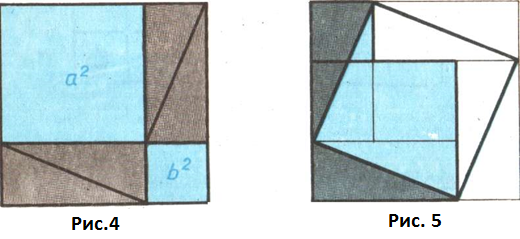
подобрать нетрудно. В самом деле, на древнекитайском чертеже четыре равных прямоугольных треугольника с катетами а, b и гипотенузой с уложены так, что их внешний контур образует квадрат со стороной а+b, а внутренний — квадрат со стороной с, построенный на гипотенузе (рис. 3). Если квадрат со стороной с вырезать и оставшиеся 4 затушеванных треугольника уложить в два прямоугольника (рис. 4), то ясно, что образовавшаяся пустота, с одной стороны, равна с², а с другой — а²+b² т.е. с² = а² + b². Теорема доказана.

                    Заметим, что при таком доказательстве построения внутри квадрата на гипотенузе, которые мы видим на древнекитайском чертеже (рис. 2), не используются. По-видимому, древнекитай­ские математики имели другое доказательство. Именно если в квадрате со стороной с два заштрихованных треугольника (рис. 3) отрезать и приложить гипотенузами к двум другим гипотенузам (рис. 5), то легко обнаружить, что полученная фигура, которую иногда называют «креслом невесты», состоит из двух квадратов со сторонами а и b, т.е. с²=а²+b².